Formas De Calcular La Distancias Entre Coordenadas En Excel

¿Te gustaría saber las formas de calcular las distancias entre coordenadas en Excel? Aquí te enseñaremos cómo calcular la distancia en Excel, usando Latitud y Longitud, en este tutorial. Te invitamos a quedarte con nosotros.

Aquí puedes aprender más sobre: Cómo Crear Un Gráfico Vectorial En Excel. 3 Pasos A Seguir

Métodos para calcular las distancias entre coordenadas en Excel

La búsqueda de una solución precisa a este problema me ha llevado a numerosos sitios e intentos de solución. Se incluye una larga lista de sitios relacionados al final de todo esto, pero los más cruciales para lo que hemos que la solución ás factible es calcular las distancias entre coordenadas en Excel.

Ahora, veamos los mejores métodos para calcular las distancias entre coordenadas en Excel:

Calcular las distancias entre coordenadas en Excel (Latitud y Longitud, Formulas)

Una fórmula que se acepta para proporcionar resultados con una precisión de milímetros se conoce como fórmula de Vincenty. Naturalmente, la precisión de los resultados depende en gran parte de la precisión de los pares de latitud/longitud que describen los dos puntos.

¿Por qué tanto alboroto por la precisión? Bueno, por lo que hemos visto de otras fórmulas, especialmente aquellas escritas como una sola función de hoja de trabajo, sus valores difieren bastante para lo que podría considerarse situaciones 'críticas para la vida'.

Mira También6 Mejores Programas Para Resolver Ecuaciones

Por lo general, son cortos por una cantidad de metros, generalmente alrededor de 20 a 30 pies por milla terrestre, y después de volar solo 30 o 40 millas, no nos importaría aterrizar varios cientos de pies antes del final de aproximación de una pista, mucho menos estar fuera por más de 7 millas en un viaje entre Los Ángeles y Honolulu.

Dado que la tendencia general al tratar con este tipo de cálculos es "medirlo con un micrómetro, marcarlo con tiza y cortarlo con un hacha", lo que tenemos aquí es un micrómetro muy preciso para comenzar el proceso de medición.

Método 1: calcular las distancias entre coordenadas en Excel (Fórmulas para la distancia)

Existen numerosas funciones de hoja de cálculo de Excel que devolverán un rumbo inicial desde un punto hasta el punto de destino para una ruta de Gran Círculo entre ellos y fórmulas similares para devolver la distancia entre ellos.

Pero según la experiencia al usarlos y compararlos con distancias medidas conocidas, el método de Vincenty para calcular las distancias entre coordenadas en Excel no se ha traducido en una sola función de hoja de cálculo, y es muy probable que no sea fácil, al menos.

Debido a que se basa en cálculos reiterativos para tratar con puntos que están muy cerca de estar exactamente en los lados opuestos del mundo, implementarlo incluso como una serie de fórmulas de hojas de cálculo de Excel es una tarea abrumadora.

Método 2: calcular las distancias entre coordenadas en Excel (Trabajar con ángulos)

Pero antes de usar la función, hay algunos pasos preliminares que se deben considerar. Lo más significativo es que Excel y VB trabajan con ángulos expresados ​​en radianes, no como valores decimales de los ángulos, ni desde su representación inicial en "inglés simple".

Mira También6 Mejores Aplicaciones de Ocio y Tiempo Libre Para Mayores

Considera esta situación:

Tienes una Latitud representada como 10° 27' 36" S (10 grados, 27 minutos 36 segundos Sur)

Necesitas convertir eso en radianes, y no hay una forma directa de hacerlo, antes de que podamos convertirlo en radianes, debe convertirse en una representación decimal. Necesitamos verlo como: 10.46 que es el decimal equivalente a 10° 27' 36" y debemos tener en cuenta si es una latitud norte o sur, y las latitudes sur se tratan como números negativos.

Afortunadamente, Microsoft proporciona un par de funciones útiles para convertir notaciones angulares estándar a su equivalente decimal, y viceversa, en esta página: Funciones de Microsoft

Esas rutinas están incluidas en la sección de código y una de ellas tiene un cambio hecho para permitir hacer una entrada de ángulo regular como

• 10~ 27' 36" S en lugar de 10° 27' 36" S

Porque ~ es directamente accesible desde el teclado, mientras que ° no lo es.

Método 3: calcular las distancias entre coordenadas en Excel (Convirtiendo a Radianes)

Después de convertir la notación estándar a un valor decimal, todavía tenemos que convertirlo a radianes y lidiar con el signo del resultado en radianes.

Mira TambiénQué Es FlexClip Usos, Características, Opiniones, Precios

Las rutinas y fórmulas aquí consideran que las latitudes negativas son latitudes del sur y las longitudes negativas son las longitudes del oeste. Si bien esto puede parecer injusto para aquellos de nosotros que vivimos en el hemisferio occidental, ¿qué puedo decir aparte de lidiar con eso?

Un valor de grados decimales se puede convertir a radianes de varias maneras en Excel y para este proceso se usa una función simple que también se incluye en el código que se presenta más adelante.

La fórmula básica es la siguiente:

• Radianes = ánguloAsDecimal x (Pi / 180)
• donde Pi es 3.14159265358979

Método 4: calcular las distancias entre coordenadas en Excel (La solución definitiva)

1. Paso 1: Copia todo el código a continuación y pégalo en un módulo de código normal en tu libro de trabajo. Las instrucciones para colocar el código en un módulo regular están aquí: Copia el código VBA de Excel en un módulo regular
2. Paso 2: Configura tu hoja de trabajo para pasar las latitudes y longitudes de los puntos inicial y final como entradas estándar
3. Paso 3: luego ingresa una fórmula para pasarlas a la función distVincenty().

Dados dos puntos con estas coordenadas:

Punto 1:

• Latitud: 37° 57' 3.7203" S
• Longitud: 144° 25' 29.5244" E

Punto 2:

• Latitud: 37° 39' 10.1561" S
• Longitud: 143° 55' 35.3839" E

El formato general de la llamada a la función es:

=distVincenty(Pt1_LatAsDecimal, Pt1_LongAsDecimal, Pt2_LatAsDecimal, Pt2_LongAsDecimal)

Mira También4 Mejores Programas Para Andar

Una fórmula sin procesar se vería así [Observe las comillas dobles después de las entradas de segundos]. La función SignIt(), proporcionada como parte del código, convierte una entrada angular estándar en un valor decimal con signo.

=distVincenty(SignIt("37° 57' 3.7203"" S "), SignIt("144° 25' 29.5244"" E"), SignIt("37° 39' 10.1561"" S"), SignIt("143° 55' 35.3839"" E"))

Puedes usar el símbolo ~ en lugar del símbolo ° si te resulta más fácil:

=distVincenty(Firmarlo("37~ 57' 3.7203"" S "), Firmarlo("144~ 25' 29.5244"" E"), Firmarlo("37~ 39' 10.1561"" S"), Firmarlo("143~ 55' 35.3839"" E"))

Si las coordenadas del Punto 1 están en B2 y C2 y las coordenadas del Punto 2 están en B3 y C3, entonces podría ingresarse como

= distVincenty (SignIt (B2), SignIt (C2), SignIt (B3), SignIt (C3))

Mira TambiénCómo Hacer Una Búsqueda VBA en Excel

El resultado de los 2 puntos de muestra utilizados anteriormente debe ser 54972,271, y este resultado está en metros.

Método 5: calcular las distancias entre coordenadas en Excel (Problemas encontrados)

El código inicial con el que comenzamos a trabajar generó errores de "fórmula demasiado compleja" en dos declaraciones. Estas declaraciones se dividieron inicialmente en dos partes y luego esos dos cálculos separados se "volvieron a unir" en una fórmula para obtener el resultado final sin el error de "fórmula demasiado compleja".

Durante la preparación de este documento, el paquete se probó en Excel 2010 de 64 bits y comenzó a devolver #¡VALOR! errores para todos los valores de entrada.

La investigación determinó que una parte de la fórmula ya dividida para determinar el valor deltaSigma estaba generando un error de desbordamiento. Este error no ocurrió en la versión de 32 bits de Excel 2010, ni en Excel 2003 (una aplicación de 32 bits).

La línea de código ofensiva se dividió una vez más en piezas más pequeñas que finalmente se volvieron a unir en un proceso matemáticamente correcto que resultó en la determinación de los valores adecuados sin recurrir a ninguna alteración del algoritmo original.

Estas secciones se indican en los comentarios del código de la función distVincenty() a continuación.

Mira TambiénCómo Usar La Función BUSCARV En Excel

El código de latitud de longitud para calcular las distancias entre coordenadas en Excel

Ahora, por fin, el código:

'*****************************************

Private Const PI = 3.14159265358979

Private Const EPSILON As Double _

    = 0.000000000001

'======================================

Public Function distVincenty(ByVal _

Mira TambiénCómo Resaltar Filas Activas en Excel

  lat1 As Double, ByVal lon1 As Double, _

    ByVal lat2 As Double, _

      ByVal lon2 As Double) As Double

'INPUTS: Latitude and Longitude of

'  initial and destination points

'  in decimal format.

Mira TambiénCómo Crear un Índice En Excel Automáticamente

'OUTPUT: Distance between the

'  two points in Meters.

'

'=============================

' Calculate geodesic distance (in m)

'  between two points specified by

'  latitude/longitude (in numeric

'  [decimal] degrees)

' using Vincenty inverse formula

'  for ellipsoids

'==============================

' Code has been ported by lost_species

'  from www.aliencoffee.co.uk to VBA

'  from javascript published at:

' https://www.movable-type.co.uk/scripts

'  /latlong-vincenty.html

' * from: Vincenty inverse formula -

'  T Vincenty, "Direct and Inverse

'  Solutions of Geodesics on the

' *       Ellipsoid with application

'  of nested equations", Survey Review,

'  vol XXII no 176, 1975

' *       https://www.ngs.noaa.gov/

'               PUBS_LIB/inverse.pdf

'Additional Reference:

'  https://en.wikipedia.org/wiki/

'      Vincenty%27s_formulae

'=============================

' Copyright lost_species 2008 LGPL

'  https://www.fsf.org/licensing/

'      licenses/lgpl.html

'=============================

' Code modifications to prevent

'  "Formula Too Complex" errors in

'  Excel (2010) VBA implementation

' provided by Jerry Latham,

'  Microsoft MVP Excel, 2005-2011

' July 23 2011

'=============================

  Dim low_a As Double

  Dim low_b As Double

  Dim f As Double

  Dim L As Double

  Dim U1 As Double

  Dim U2 As Double

  Dim sinU1 As Double

  Dim sinU2 As Double

  Dim cosU1 As Double

  Dim cosU2 As Double

  Dim lambda As Double

  Dim lambdaP As Double

  Dim iterLimit As Integer

  Dim sinLambda As Double

  Dim cosLambda As Double

  Dim sinSigma As Double

  Dim cosSigma As Double

  Dim sigma As Double

  Dim sinAlpha As Double

  Dim cosSqAlpha As Double

  Dim cos2SigmaM As Double

  Dim C As Double

  Dim uSq As Double

  Dim upper_A As Double

  Dim upper_B As Double

  Dim deltaSigma As Double

  Dim s As Double ' final result,

'  will be returned rounded to

'  3 decimals (mm).

'added by JLatham to break up

'  "Too Complex" formulas

'into pieces to properly calculate

'  those formulas as noted below

'and to prevent overflow errors when

'  using Excel 2010 x64 on

'  Windows 7 x64 systems

  Dim P1 As Double ' used to calculate

'  a portion of a complex formula

  Dim P2 As Double ' used to calculate

'  a portion of a complex formula

  Dim P3 As Double ' used to calculate

'  a portion of a complex formula

'See https://en.wikipedia.org/wiki

'  /World_Geodetic_System

'for information on various Ellipsoid

'  parameters for other standards.

'low_a and low_b in meters

' === GRS-80 ===

' low_a = 6378137

' low_b = 6356752.314245

' f = 1 / 298.257223563

'

' === Airy 1830 ===  Reported best

'  accuracy for England

'  and Northern Europe.

' low_a = 6377563.396

' low_b = 6356256.910

' f = 1 / 299.3249646

'

' === International 1924 ===

' low_a = 6378388

' low_b = 6356911.946

' f = 1 / 297

'

' === Clarke Model 1880 ===

' low_a = 6378249.145

' low_b = 6356514.86955

' f = 1 / 293.465

'

' === GRS-67 ===

' low_a = 6378160

' low_b = 6356774.719

' f = 1 / 298.247167

'== WGS-84 Ellipsoid Parameters ===

  low_a = 6378137       ' +/- 2m

  low_b = 6356752.3142

  f = 1 / 298.257223563

'=========================

  L = toRad(lon2 - lon1)

  U1 = Atn((1 - f) * Tan(toRad(lat1)))

  U2 = Atn((1 - f) * Tan(toRad(lat2)))

  sinU1 = Sin(U1)

  cosU1 = Cos(U1)

  sinU2 = Sin(U2)

  cosU2 = Cos(U2)

  lambda = L

  lambdaP = 2 * PI

  iterLimit = 100 ' can be set

'  as low as 20 if desired.

  While (Abs(lambda - lambdaP) > _

      EPSILON) And (iterLimit > 0)

    iterLimit = iterLimit - 1

    sinLambda = Sin(lambda)

    cosLambda = Cos(lambda)

    sinSigma = Sqr(((cosU2 * sinLambda) _

        ^ 2) + ((cosU1 * sinU2 - sinU1 _

        * cosU2 * cosLambda) ^ 2))

    If sinSigma = 0 Then

     distVincenty = 0 'co-incident points

      Exit Function

    End If

    cosSigma = sinU1 * sinU2 + cosU1 _

      * cosU2 * cosLambda

    sigma = Atan2(cosSigma, sinSigma)

    sinAlpha = cosU1 * cosU2 * _

      sinLambda / sinSigma

    cosSqAlpha = 1 - sinAlpha * sinAlpha

    If cosSqAlpha = 0 Then 'check for

    'a divide by zero

      cos2SigmaM = 0 '2 points on equator

    Else

      cos2SigmaM = cosSigma - 2 _

        * sinU1 * sinU2 / cosSqAlpha

    End If

    C = f / 16 * cosSqAlpha * (4 + f _

        * (4 - 3 * cosSqAlpha))

    lambdaP = lambda

'the original calculation is

'  "Too Complex" for Excel VBA

'  to deal with

'so it is broken into segments

'  to calculate without that issue

'the original implementation

'  to calculate lambda

'lambda = L + (1 - C) * f * sinAlpha * _

  (sigma + C * sinSigma * (cos2SigmaM

'  + C * cosSigma * (-1 + 2

'  * (cos2SigmaM ^ 2))))

      'calculate portions

    P1 = -1 + 2 * (cos2SigmaM ^ 2)

    P2 = (sigma + C * sinSigma * _

      (cos2SigmaM + C * cosSigma * P1))

    'complete the calculation

    lambda = L + (1 - C) * f _

      * sinAlpha * P2

  Wend

  If iterLimit > 1 Then

   MsgBox _

   "iteration limit has been reached," _

        & " something didn't work."

    Exit Function

  End If

  uSq = cosSqAlpha * (low_a ^ 2 _

    - low_b ^ 2) / (low_b ^ 2)

'the original calculation is

'  "Too Complex" for Excel VBA

'  to deal with

'so it is broken into segments to

'  calculate without that issue

  'the original implementation to

'  calculate upper_A

  'upper_A = 1 + uSq / 16384 *

'  (4096 + uSq * (-768 + uSq *

'  (320 - 175 * uSq)))

  'calculate one piece of the equation

  P1 = (4096 + uSq * (-768 _

    + uSq * (320 - 175 * uSq)))

  'complete the calculation

  upper_A = 1 + uSq / 16384 * P1

  'oddly enough, upper_B calculates

'  without any issues - JLatham

  upper_B = uSq / 1024 * (256 + uSq _

    * (-128 + uSq * (74 - 47 * uSq)))

'the original calculation is

'  "Too Complex" for Excel VBA

'  to deal with

'so it is broken into segments to

'  calculate without that issue

  'the original implementation to

'  calculate deltaSigma

  'deltaSigma = upper_B * sinSigma *

'  (cos2SigmaM + upper_B / 4 *

'  (cosSigma * (-1 + 2

'   * cos2SigmaM ^ 2) _

     - upper_B / 6 * cos2SigmaM *

'   (-3 + 4 * sinSigma ^ 2) *

'   (-3 + 4 *cos2SigmaM ^ 2)))

  'calculate pieces of the

'  deltaSigma formula

  'broken into 3 pieces to prevent

'  overflow error that may occur in

  'Excel 2010 64-bit version.

  P1 = (-3 + 4 * sinSigma ^ 2) * _

    (-3 + 4 * cos2SigmaM ^ 2)

  P2 = upper_B * sinSigma

  P3 = (cos2SigmaM + upper_B / 4 * _

   (cosSigma * (-1 + 2 _

      * cos2SigmaM ^ 2) - _

     upper_B / 6 * cos2SigmaM * P1))

  'complete deltaSigma calculation

  deltaSigma = P2 * P3

  'calculate the distance

  s = low_b * upper_A * _

    (sigma - deltaSigma)

  'round distance to millimeters

  distVincenty = Round(s, 3)

End Function

'======================================

Function SignIt(Degree_Dec As String) _

    As Double

'Input:  a string representation of

'  a lat or long in the

'         format of 10° 27' 36" S/N

'  or 10~ 27' 36" E/W

'OUTPUT:  signed decimal value

'  ready to convert to radians

'

  Dim decimalValue As Double

  Dim tempString As String

  tempString = UCase(Trim(Degree_Dec))

  decimalValue = _

    Convert_Decimal(tempString)

  If Right(tempString, 1) = "S" _

    Or Right(tempString, 1) = "W" Then

    decimalValue = decimalValue * -1

  End If

  SignIt = decimalValue

End Function

'======================================

Function Convert_Degree(Decimal_Deg) _

  As Variant

'source: https://support.microsoft.com/

'  kb/213449

'

'converts a decimal degree

'  representation to deg min sec

'as 10.46 returns 10° 27' 36"

'

  Dim degrees As Variant

  Dim minutes As Variant

  Dim seconds As Variant

  With Application

     'Set degree to Integer of

'  Argument Passed

     degrees = Int(Decimal_Deg)

     'Set minutes to 60 times the

'  number to the right

     'of the decimal for the

'  variable Decimal_Deg

     minutes = (Decimal_Deg - _

    degrees) * 60

     'Set seconds to 60 times the

'  number to the right of the

     'decimal for the variable Minute

     seconds = Format(((minutes - _

    Int(minutes)) * 60), "0")

     'Returns the Result of degree

'  conversion

    '(for example, 10.46 = 10° 27' 36")

     Convert_Degree = " " & degrees _

    & "° " & Int(minutes) & "' " _

         & seconds + Chr(34)

  End With

End Function

'======================================

Function Convert_Decimal _

    (Degree_Deg As String) As Double

'source: https://support.microsoft.com/

'  kb/213449

   ' Declare the variables to be

'  double precision floating-point.

   ' Converts text angular entry to

'  decimal equivalent, as:

   ' 10° 27' 36" returns 10.46

   ' alternative to ° is permitted:

'  Use ~ instead, as:

   ' 10~ 27' 36" also returns 10.46

   Dim degrees As Double

   Dim minutes As Double

   Dim seconds As Double

   '

   'modification by JLatham

   'allow the user to use the ~

'  symbol instead of ° to denote degrees

   'since ~ is available from the

'  keyboard and ° has to be entered

   'through [Alt] [0] [1] [7] [6]

'  on the number pad.

   Degree_Deg = Replace(Degree_Deg, _

    "~", "°")

   ' Set degree to value before

'  "°" of Argument Passed.

   degrees = Val(Left(Degree_Deg, _

    InStr(1, Degree_Deg, "°") - 1))

   ' Set minutes to the value between

'  the "°" and the "'"

   ' of the text string for the variable

'   Degree_Deg divided by

   ' 60. The Val function converts the

'   text string to a number.

   minutes = Val(Mid(Degree_Deg, _

    InStr(1, Degree_Deg, "°") + 2, _

      InStr(1, Degree_Deg, "'") - _

    InStr(1, Degree_Deg, "°") - 2)) / 60

   ' Set seconds to the number to the

'  right of "'" that is

   ' converted to a value and then

'  divided by 3600.

   seconds = Val(Mid(Degree_Deg, _

    InStr(1, Degree_Deg, "'") + _

      2, Len(Degree_Deg) - _

    InStr(1, Degree_Deg, "'") - 2)) _

    / 3600

   Convert_Decimal = degrees _

    + minutes + seconds

End Function

'======================================

Private Function toRad(ByVal _

    degrees As Double) As Double

    toRad = degrees * (PI / 180)

End Function

'======================================

Private Function Atan2( _

    ByVal X As Double, _

    ByVal Y As Double) As Double

 ' code nicked from:

 ' https://en.wikibooks.org/wiki/

'  Programming:Visual_Basic_Classic/

'  Simple_Arithmetic

'  #Trigonometrical_Functions

 ' If you re-use this watch out:

'  the x and y have been reversed from

'  typical use.

    If Y > 0 Then

        If X >= Y Then

            Atan2 = Atn(Y / X)

        ElseIf X <= -Y Then

            Atan2 = Atn(Y / X) + PI

        Else

        Atan2 = PI / 2 - Atn(X / Y)

    End If

        Else

            If X >= -Y Then

            Atan2 = Atn(Y / X)

        ElseIf X <= Y Then

            Atan2 = Atn(Y / X) - PI

        Else

            Atan2 = -Atn(X / Y) - PI / 2

        End If

    End If

End Function

'======================================

Cómo calcular las distancias entre coordenadas en Excel con la fórmula de distancia

Ahora, veamos cómo calcular las distancias entre coordenadas en Excel con la fórmula de distancia:

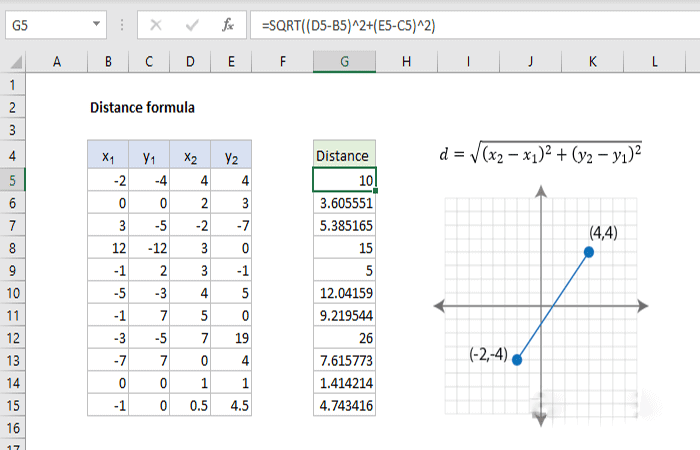
La fórmula genérica es la siguiente = RAÍZ CUADRADA (( x2 - x1 ) ^ 2 + ( y2 - y1 ) ^ 2 )

Resumen

Para calcular la longitud de una línea 2D dadas las coordenadas de dos puntos en la línea, puede usar la fórmula de distancia, adaptada para la sintaxis de fórmula de Excel. En el ejemplo que se muestra, la fórmula en G5, copiada hacia abajo, es:

= SQRT (( D5 - B5 ) ^ 2 + ( E5 - C5 ) ^ 2 )

donde las coordenadas de los dos puntos se dan en las columnas B a E.

Explicación

La longitud de una línea se puede calcular con la fórmula de la distancia, que se ve así:

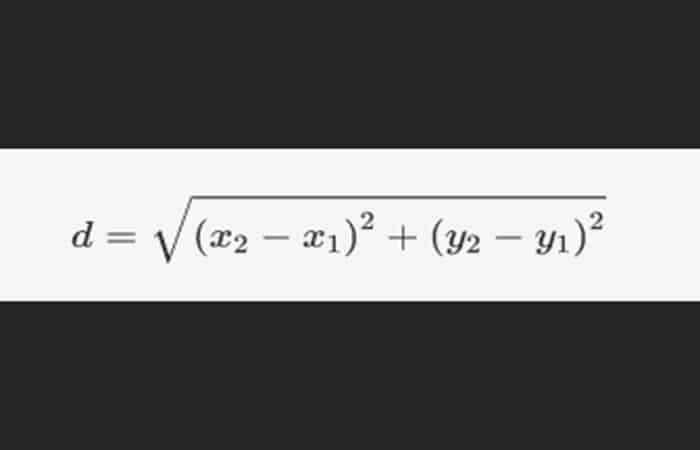
La distancia es la raíz cuadrada del cambio en x al cuadrado más el cambio en y al cuadrado, donde se dan dos puntos en la forma (x 1, y 1 ) y (x 2 , y 2 ). La fórmula de la distancia es un ejemplo de la aplicación del Teorema de Pitágoras, donde el cambio en x y el cambio en y corresponden a los dos lados de un triángulo rectángulo, y la hipotenusa es la distancia que se calcula.

En Excel, la fórmula de la distancia se puede escribir con el operador exponente (^) y la función SQRT es la siguiente:

• = SQRT (( D5 - B5 ) ^ 2 + ( E5 - C5 ) ^ 2 )

Siguiendo el orden de operaciones de Excel, se calcula el cambio en x y el cambio en y, luego se elevan al cuadrado, y los dos resultados se suman y se envían a la función SQRT, que devuelve la raíz cuadrada de la suma como resultado final:

= SQRT (( D5 - B5 ) ^ 2 + ( E5 - C5 ) ^ 2 )

= SQRT (( 6 ) ^ 2 + ( 8 ) ^ 2 )

= SQRT ( 36 + 64 )

= SQRT ( 100 )

= 10

La función POTENCIA también se puede usar en lugar del operador exponente (^) de esta manera:

= SQRT ( POTENCIA ( D5 - B5 , 2 ) + POTENCIA ( E5 - C5 , 2 ))

con el mismo resultado.

Métodos para calcular las distancias entre coordenadas en Excel (distancia, convertir grados y geocodificar direcciones)

Si tienes una larga lista de coordenadas geográficas para trabajar, una hoja de cálculo de Microsoft Excel seguramente será útil. Hay tres herramientas básicas de Excel que pueden funcionar para ti, sin importar cómo quieras manipular las coordenadas geográficas.

Necesitarás saber cómo calcular las distancias entre coordenadas en Excel, cómo convertir datos de latitud y longitud a grados decimales y, finalmente, cómo geocodificar latitudes y longitudes.

Método 1: calcular las distancias entre coordenadas en Excel

En un ejemplo de cómo calcular la distancia entre dos coordenadas en Excel, buscaremos medir la distancia del gran círculo. Notaremos que la latitud y la longitud se denotan en grados, minutos y segundos.

Cómo calcular las distancias entre coordenadas en Excel al convertir latitud y longitud a grados decimales

Todo, incluso algo tan complicado como grados, minutos y segundos, se puede convertir a decimales. La parte de los grados sigue siendo la misma, pero los minutos y los segundos deben convertirse a su porcentaje de un grado y combinarse.

Hay 60 minutos en un grado y 60 segundos en un minuto (lo que significa 3600 segundos en un grado). Por tanto, se dividen los minutos entre 60 y los segundos entre 3.600.

La fórmula general:

• Grados totales (en forma decimal) = Grados + [Minutos/60] + [Segundos/3600]

…Sobre esa distancia

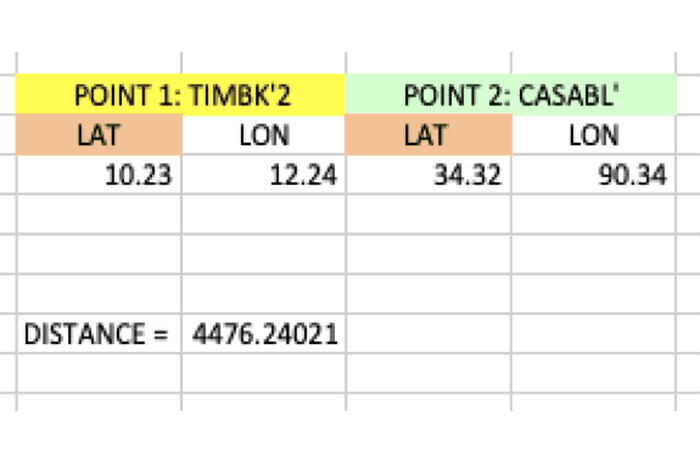
Ahora que tienes los valores de latitud y longitud en decimales, solo enfrentas la ecuación de las millas náuticas entre Tombuctú y Casablanca, que se indica a continuación.

Millas náuticas = ACOS [(sin(Lat_place_1*PI()/180)*sin(Lat_place_2*PI()/180)+ cos(Lat_place_1*PI()/180)*cos(Lat_place_2*PI()/180)* cos(Lon_place_2*PI()/180-Lon_place_1*PI()/180)) ] *3443.8985

Ese número tres mil, al final, es el radio de la Tierra, en Millas Náuticas. Incluso si tuviera que sustituirlo por el radio de una esfera, suponiendo que la Tierra es esférica, a 3437,7468 NM, no estará cerca de la distancia real y precisa.

Método 2: calcular las distancias entre coordenadas en Excel (Geocodificar latitud y longitud)

La geocodificación es la conversión de direcciones de calles a datos de latitud y longitud que se pueden mapear. Ahora, hay dos formas de geocodificar la latitud y la longitud desde una hoja de cálculo de Excel: la forma difícil y la forma fácil.

Primero cubriremos la manera difícil, que es lo que necesitarás si quieres que las coordenadas vivan en tu documento de Excel. Deberás escribir la secuencia de comandos de Visual Basic (VBA) para realizar una llamada a un geocodificador externo o buscar el código en otro lugar. Hay varias API de geocodificadores y algunos geocodificadores son más rápidos que otros.

La API de codificación geográfica de Google Maps es una opción común y esta es la API que llamaremos en la opción fácil. Sin embargo, también puedes funcionar directamente dentro de Excel. Armado con el código que has escrito o descubierto, estos son los pasos para implementar la geocodificación en Excel.

La forma difícil

1. Paso 1:busca la pestaña Desarrollador en tu versión de Excel.
2. Paso 2:busca la pestaña "Visual Basic". Esto abre la ventana de desarrollo.
3. Paso 3:Insertar —> Módulo. El nuevo módulo mantendrá tu función.
4. Paso 4: Aquí es donde copias y pegas tu código.
5. Paso 5:Necesitamos agregar referencias ahora. Entonces, Herramientas —> Referencias. Asegúrate de verificar Microsoft XML v6.0. HAZ CLIC EN ACEPTAR.
6. Paso 6:Presiona CTRL / CMD + S. Guardar como tipo —> Complemento de Excel. Ahora puedes nombrar tu función. La extensión tiene que ser xlam. Es hora de cerrar todos los archivos de Excel.
7. Paso 7:Abre un nuevo archivo siguiendo la siguiente ruta: Archivo —> Opciones —> Complementos. En el cuadro Administrar, elige Complementos de Excel.
8. Paso 8:Presiona Ir. Elige la función en la ventana que aparece marcando la casilla. Presiona
9. Paso 9:Ahora podrías usar la nueva función que creaste, como cualquier otra función.

NOTA: Una vez que hayas terminado de recuperar los valores, cópialos y pégalos en otro lugar, fuera de la hoja con los cálculos. Luego, elimina las llamadas de función porque, de lo contrario, cuando vuelve a abrir este archivo, la API de Google comenzará a recibir un ping nuevamente. Eso consumirá varios minutos antes de que se abra el archivo. Para optimizar el uso de recursos de Google, tome un descanso de 10 segundos entre direcciones.

Son muchos pasos y se supone que ha encontrado algún código para probar. A continuación, veremos la forma más fácil de geocodificar tus datos de Excel. Es rápido y confiable, pero no importará las coordenadas a su archivo de Excel. Por otro lado, la herramienta de geocodificación de Excel es simple de copiar y pegar y te brinda un mapa interactivo.

La forma fácil (calcular las distancias entre coordenadas en Excelal crear un mapa)

Hay varias formas de crear mapas con datos de Excel. Quizás lo más fácil es simplemente copiar y pegar los datos de tu hoja de cálculo en nuestra herramienta de creación de mapas. Al hacerlo, convierte tu documento de Excel en un hermoso mapa interactivo.

1. Paso 1: Para hacer tu propio mapa basado en las coordenadas de latitud y longitud, separe las coordenadas en tus propias columnas dentro de tu hoja de cálculo.

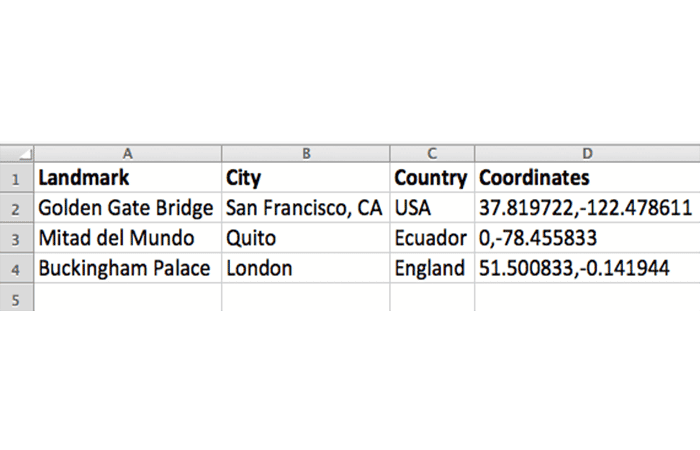
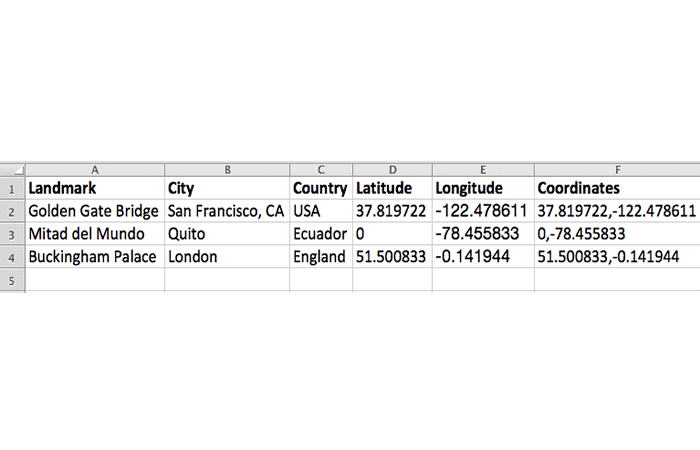
2. Paso 2: Luego, selecciona y copia las filas y columnas de tu hoja de cálculo (comando Ctrl+C o Cmd+C en Mac) y Pega (Ctrl+V o Cmd+V en Mac) en tus datos, ¡y listo!

También te puede interesar leer sobre: Cómo Usar La Función CUARTIL En Excel - Guía Completa

Conclusión

Como puedes ver, estos son los métodos que puedes utilizar para para calcular las distancias entre coordenadas en Excel. Ya sea que quieras crear un mapa de latitud y longitud o crear tu propia guía virtual de bodas para tus invitados, Estos procesos ofrecen una forma fácil y gratuita de crear hermosos mapas web que están listos para guardar y compartir. Esperamos haberte ayudado con esta información.