Fórmulas con matrices en Excel: guía completa y ejemplos prácticos

Las fórmulas con matrices en Excel son de esas herramientas que parecen “magia negra” la primera vez que las ves, pero que, cuando las dominas, te permiten hacer en una sola fórmula lo que antes requería decenas o cientos de celdas de ayuda.

Aunque al principio puedan imponer un poco de respeto, las matrices y las fórmulas matriciales son uno de los recursos más potentes de Excel para análisis de datos, modelización, finanzas, ingeniería o simplemente para dejar tus hojas mucho más limpias y rápidas.

Qué es una matriz y qué es una fórmula matricial en Excel

En Excel, una matriz no es más que una colección de valores que se tratan como un conjunto: pueden estar en una sola fila, en una sola columna o formar un bloque de varias filas y columnas.

Por ejemplo, una matriz muy típica podría contener los meses del año escritos uno debajo de otro o uno al lado de otro, y Excel trabajaría con ese grupo como si fuese un único objeto de datos.

Una fórmula matricial es una fórmula que, en lugar de operar con un único valor, trabaja simultáneamente con una matriz completa de elementos: puede realizar varios cálculos a la vez y devolver un único resultado o una matriz de resultados.

La idea clave es que una fórmula matricial hace que Excel procese muchos elementos en bloque, evaluando internamente todos los valores y, si hace falta, devolviendo también varios resultados a la vez en distintas celdas.

Por ejemplo, imagina que tienes en la columna B el número de unidades vendidas y en la columna C el precio de cada unidad. Con una fórmula matricial como =SUMA(B2:B11*C2:C11), Excel multiplica cada fila (unidades por precio) y después suma todos esos productos, sin necesidad de columnas intermedias.

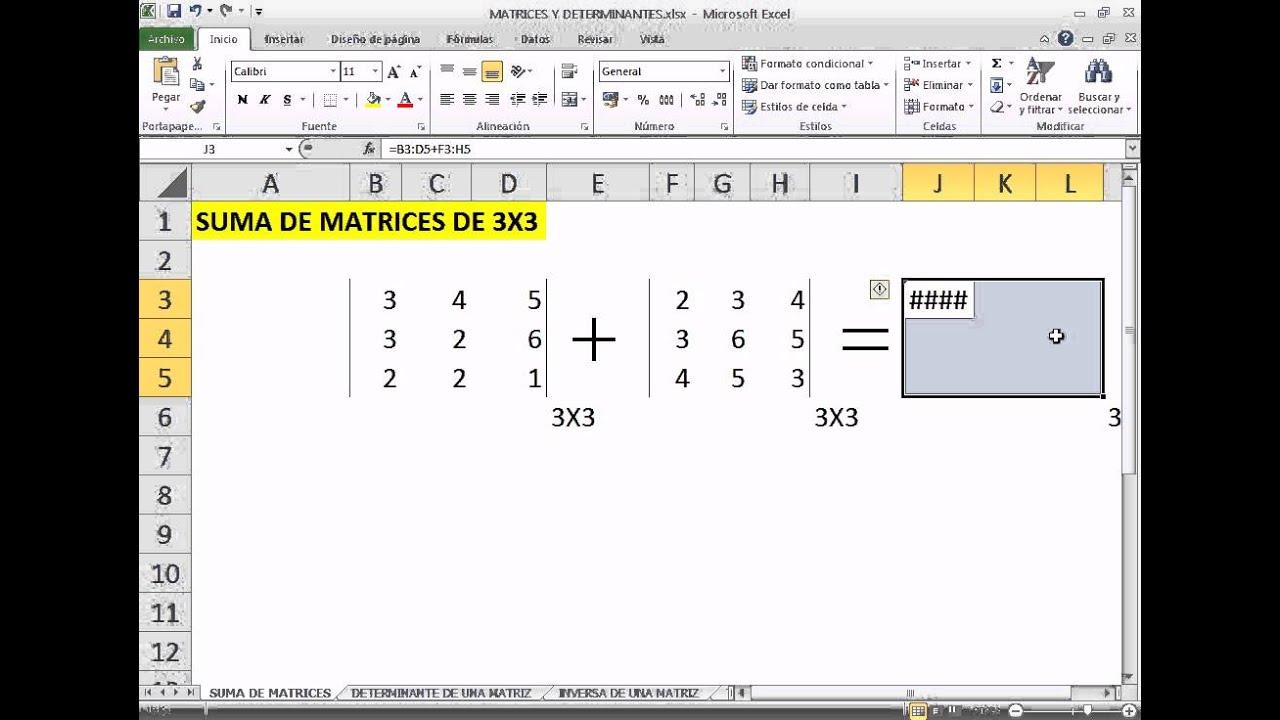
Cómo introducir y reconocer una fórmula matricial clásica

Las fórmulas matriciales “de toda la vida” en Excel se introducen con una combinación de teclas especial: Ctrl + Mayús + Intro (Ctrl + Shift + Enter). No basta con pulsar Intro normal.

Cuando escribes una fórmula matricial y confirmas con esa combinación, Excel muestra la fórmula en la barra de fórmulas rodeada por llaves { }. Esas llaves no se escriben a mano: Excel las añade automáticamente al detectar que es una fórmula matricial.

Si intentas teclear tú mismo las llaves, Excel no la tratará como una fórmula de matriz, sino como una fórmula normal, así que es obligatorio usar la combinación de teclas para que funcione.

Cada vez que edites una fórmula matricial, las llaves desaparecen temporalmente: tendrás que volver a pulsar Ctrl + Mayús + Intro al terminar la edición, o la fórmula dejará de ser matricial y solo se calculará sobre el primer elemento del rango.

Y un detalle importante: si se te olvida usar la combinación y pulsas solo Intro, la fórmula se comportará como una fórmula estándar, tomando solo el primer valor de cada rango, lo que puede dar resultados erróneos sin que te des cuenta.

Tipos de fórmulas matriciales: un resultado o varios resultados

Podemos distinguir dos grandes tipos de fórmulas con matrices en Excel: las que devuelven un único valor y las que devuelven un conjunto de resultados repartidos en varias celdas.

En el primer caso, la fórmula toma una matriz de datos, realiza los cálculos y devuelve un solo resultado en una celda (por ejemplo, una suma, una media, una cuenta, un mínimo o un máximo).

En el segundo tipo, la propia fórmula genera una matriz de salida que ocupa dos o más celdas. En este caso, todos los resultados forman parte de una sola fórmula matricial que “vive” en varias celdas a la vez.

Funciones como SUMA, PROMEDIO, MAX o MIN (y en sus variantes, MINIFS y MAXIFS) pueden trabajar con matrices si se introducen como fórmulas matriciales en una sola celda, mientras que otras, como TRANSPONER, TENDENCIA o FRECUENCIA, están diseñadas para devolver matrices de varias celdas.

Lo potente de todo esto es que una sola fórmula puede sustituir a muchas columnas auxiliares, manteniendo tu hoja más limpia, más ligera y con menos riesgo de errores de copia o de actualización.

Ejemplos avanzados de fórmulas matriciales clásicas

Las fórmulas de matriz permiten resolver situaciones que con fórmulas normales serían engorrosas o directamente imposibles. A continuación se recogen varios ejemplos típicos y avanzados basados en rangos con nombres como Datos, Ventas, MisDatos o TusDatos.

Sumar rangos que contienen errores

Cuando un rango incluye errores como #N/A, una suma normal con SUMA falla. Con una fórmula matricial puedes ignorar esos errores y sumar solo los valores válidos:

=SUMA(SI(ESERROR(Datos),»»,Datos))

La función ESERROR detecta las celdas con error dentro del rango Datos y la función SI crea una nueva matriz donde, en lugar de los errores, coloca cadenas vacías «», y donde las celdas sin error conservan su valor original.

Sobre esa matriz limpia, la función SUMA calcula el total ignorando los elementos vacíos, de modo que consigues obtener el sumatorio aunque el rango original tenga celdas defectuosas.

Contar cuántos errores hay en un rango

Si lo que necesitas es contar los errores en lugar de sumarlos, puedes usar una variante similar:

=SUMA(SI(ESERROR(Datos),1,0))

Esta fórmula construye una matriz en la que cada celda con error se transforma en un 1 y cada celda sin error en un 0, de forma que la suma de todos esos 1 y 0 te da el número total de errores.

La fórmula puede simplificarse eliminando el tercer argumento de SI, ya que cuando la condición es falsa devuelve FALSO, y SUMA interpreta FALSO como 0:

=SUMA(SI(ESERROR(Datos),1))

Y todavía es posible acortarla más multiplicando directamente el resultado booleano por 1, aprovechando que VERDADERO*1=1 y FALSO*1=0:

=SUMA(SI(ESERROR(Datos)*1))

Sumar valores que cumplen condiciones (AND y OR “a mano”)

Con fórmulas matriciales puedes sumar solo los valores que cumplan determinadas condiciones sin necesidad de recurrir siempre a SUMAR.SI.CONJUNTO. Por ejemplo, para sumar solo los valores positivos del rango Ventas:

=SUMA(SI(Ventas>0;Ventas))

Aquí la función SI genera una matriz donde las celdas con un valor mayor que 0 mantienen su valor y las demás se convierten en FALSO; la función SUMA ignora los FALSO y suma únicamente los números positivos.

También puedes combinar varias condiciones mediante multiplicaciones (equivalente a un Y lógico) o sumas (equivalente a un O lógico). Por ejemplo, para sumar valores mayores que 0 y menores o iguales que 5:

=SUMA((Ventas>0)*(Ventas<=5)*(Ventas))

En este caso, las expresiones lógicas devuelven matrices de VERDADERO/FALSO, que al multiplicarse se convierten en 1 o 0 y actúan como filtros sobre los valores de Ventas.

Si lo que necesitas es un comportamiento de tipo O, puedes usar la suma de condiciones lógicas dentro de SI, como en esta fórmula que suma valores menores de 5 o mayores de 15:

=SUMA(SI((Ventas<5)+(Ventas>15);Ventas))

Las funciones Y y O devuelven un único VERDADERO o FALSO, por lo que no se usan directamente con matrices múltiples; la solución es emularlas con multiplicaciones y sumas como en los ejemplos anteriores.

Calcular una media excluyendo ceros

Si quieres obtener un promedio sin tener en cuenta los ceros, puedes combinar PROMEDIO con una condición matricial sobre el rango Ventas:

=PROMEDIO(SI(Ventas<>0;Ventas))

La matriz resultante de SI contiene únicamente los valores distintos de 0, que son los que finalmente utiliza PROMEDIO para calcular la media.

Contar diferencias entre dos rangos

Supón que tienes dos rangos con el mismo tamaño y forma, llamados MisDatos y TusDatos, y quieres saber en cuántas celdas difieren. Una fórmula matricial lo resuelve así:

=SUMA(SI(MisDatos=TusDatos,0,1))

La función SI genera una matriz en la que cada coincidencia se convierte en un 0 y cada discrepancia en un 1. Al sumar la matriz obtienes el recuento de celdas diferentes.

También aquí existe una versión más compacta que usa directamente la comparación desigual (<>) multiplicada por 1:

=SUMA(1*(MisDatos<>TusDatos))

De nuevo se aprovecha el truco de que VERDADERO equivale a 1 y FALSO a 0 cuando se multiplican por un número.

Localizar el máximo y su posición en un rango

Con fórmulas matriciales no solo puedes saber cuál es el valor máximo de un conjunto, sino también su posición exacta en la hoja; también puedes usar la función RANK para ordenar y localizar posiciones.

Para encontrar el número de fila del máximo dentro del rango de una columna con nombre Datos puedes usar:

=MIN(SI(Datos=MAX(Datos),FILA(Datos),»»))

Esta fórmula crea una matriz donde las celdas que contienen el valor máximo guardan su número de fila y el resto quedan como cadenas vacías. La función MIN busca el menor número de esa matriz, que coincide con la primera fila donde aparece el máximo.

Si lo que quieres es obtener directamente la referencia de la celda del máximo, puedes envolver el cálculo anterior con DIRECCION y COLUMNA:

=DIRECCION(MIN(SI(Datos=MAX(Datos),FILA(Datos),»»)),COLUMNA(Datos))

Crear fórmulas matriciales de varias celdas paso a paso

En un libro de ejemplo con una tabla de vendedores, tipos de vehículo, unidades vendidas y precios, se puede ilustrar cómo funciona una fórmula matricial que ocupa varias celdas a la vez.

Imagina que has copiado una tabla a partir de la celda A1 con estos campos: Vendedor, Tipo de vehículo, Número vendido, Precio unitario y Ventas totales, y que en la columna E quieres calcular las ventas de cada línea mediante una fórmula de matriz.

En el rango C2:C11 tienes las cantidades vendidas y en D2:D11 los precios; el objetivo es llenar E2:E11 con el producto de cada fila sin escribir fórmulas una por una.

Para hacerlo como fórmula matricial de varias celdas, primero selecciona todo el rango E2:E11, escribe en la barra de fórmulas:

=C2:C11*D2:D11

y confirma con Ctrl + Mayús + Entrar. Excel rellenará de golpe todas las celdas de E2 a E11 con el resultado correspondiente a cada fila.

Fórmula matricial de una sola celda sobre el mismo ejemplo

Partiendo de esa misma tabla, es posible obtener el total general de ventas mediante una única fórmula matricial en una sola celda, por ejemplo B13.

En lugar de escribir fórmulas fila a fila, basta con introducir en B13:

=SUMA(C2:C11*D2:D11)

y confirmar con Ctrl + Mayús + Entrar. Excel realiza internamente la multiplicación de cada par de celdas Cx*Dx, y luego suma todos esos productos para dar el total.

Cómo depurar y entender una fórmula matricial compleja

Cuando una fórmula resulta larga y un poco “críptica”, es fundamental poder ver qué está calculando cada parte. Excel permite evaluar fragmentos de una fórmula usando la tecla F9.

El truco consiste en seleccionar, dentro de la barra de fórmulas, una porción concreta (por ejemplo, solo B2:B11*C2:C11), y a continuación pulsar F9 para que Excel sustituya temporalmente ese fragmento por el resultado intermedio.

Al hacer esto en una fórmula matricial, verás desplegarse la matriz resultante, con todos sus elementos, lo que ayuda mucho a entender el comportamiento de la fórmula y a localizar posibles errores.

Una vez que hayas inspeccionado la parte elegida, puedes pulsar Esc para salir sin guardar los cambios, o Ctrl + Z si has confirmado por accidente y quieres deshacer la evaluación.

Matrices constantes en Excel: cómo crearlas y usarlas

Además de usar rangos de celdas, Excel permite trabajar con constantes matriciales, que son conjuntos de valores fijos escritos directamente dentro de una fórmula y que no cambian al copiar ni desplazar la fórmula.

Una constante matricial puede contener números, textos, valores lógicos (VERDADERO/FALSO) o errores, pero no puede incluir referencias de celda, nombres definidos, fechas, funciones u otras matrices.

Existen constantes unidimensionales horizontales (una sola fila), unidimensionales verticales (una sola columna y bidimensionales (un bloque de filas y columnas), y se distinguen por los separadores que se utilizan entre los elementos.

En configuraciones regionales en español, las matrices verticales suelen separar elementos con punto y coma (;), mientras que en matrices horizontales puede emplearse otro separador (en algunas configuraciones, la barra invertida) o la coma, según la configuración del sistema.

Por ejemplo, una matriz vertical con los meses del año podría expresarse como:

={«Enero»;»Febrero»;»Marzo»;»Abril»;»Mayo»;»Junio»;»Julio»;»Agosto»;»Septiembre»;»Octubre»;»Noviembre»;»Diciembre»}

Asignar un nombre a una constante matricial

Para hacer más manejable el uso de una constante grande, puedes asignarle un nombre con el Administrador de nombres de Excel, de esta manera la reutilizas sin volver a escribirla.

El proceso es sencillo: entras en la ficha Fórmulas, usas la opción de Nombre definido o Asignar nombre, escribes el nombre deseado y, en el cuadro “Se refiere a”, introduces directamente la constante matricial.

Por ejemplo, podrías crear un nombre llamado Meses que apunte a la constante:

={«Enero»\»Febrero»\»Marzo»\»Abril»\»Mayo»\»Junio»\»Julio»\»Agosto»\»Septiembre»\»Octubre»\»Noviembre»\»Diciembre»}

Después, basta con seleccionar tantas celdas como elementos tenga la matriz, escribir el nombre =Meses y confirmar como fórmula matricial para que aparezcan todos los valores distribuidos en la hoja.

Si la constante da problemas, es buena idea revisar los separadores utilizados y que se ha seleccionado un rango adecuado al tamaño de la matriz antes de introducir la fórmula con Ctrl + Mayús + Entrar.

Ejemplos de uso de constantes matriciales

Las constantes permiten construir fórmulas potentes en muy poco espacio. Por ejemplo, para sumar los tres valores más altos de un rango puedes usar una combinación con K.ESIMO.MAYOR y una constante que defina los órdenes deseados.

De forma análoga, es posible sumar los N valores más pequeños con K.ESIMO.MENOR, simplemente cambiando la función pero manteniendo la matriz de posiciones que quieras sumar.

Otro caso típico es contar cuántas veces un evaluador (por ejemplo, Pedro) ha puntuado con varios valores concretos sin tener que repetir criterios en CONTAR.SI.CONJUNTO una y otra vez.

En un rango de evaluaciones podrías usar una fórmula de este estilo:

=SUMA(CONTAR.SI.CONJUNTO(A2:A28;»Pedro»;C2:C28;{3\4\5}))

Aquí, la constante {3\4\5} recoge las puntuaciones aceptadas (3, 4 y 5) y hace que la fórmula sea más compacta y fácil de mantener, aunque podrías ampliarla con más valores si fuera necesario, respetando siempre el límite máximo de caracteres de una fórmula.

Fórmulas de matrices dinámicas en Excel 365 y 2021

Con las versiones modernas de Excel (Microsoft 365 y Excel 2021) se introdujo un cambio muy importante: las fórmulas de matrices dinámicas, que eliminan la necesidad de usar Ctrl + Mayús + Entrar en la mayoría de los casos.

Estas nuevas fórmulas trabajan de forma nativa con rangos y matrices y tienen la capacidad de “desbordarse” automáticamente sobre las celdas adyacentes, ocupando tantas filas y columnas como haga falta para mostrar todos los resultados.

La gran diferencia es que solo escribes la fórmula en una celda y pulsas Intro normal; Excel rellena el rango de salida que necesite, y lo marca con un borde especial que indica que se trata de un rango de desbordamiento.

Además, han aparecido nuevas funciones diseñadas específicamente para trabajar con matrices dinámicas, como FILTRAR, ORDENAR, ÚNICO, SECUENCIA, ORDENARPOR o MATRIZALEATORIA, entre otras.

Estas funciones permiten filtrar, ordenar, generar listas secuenciales o números aleatorios, y devolver conjuntos de resultados sin necesidad de definir previamente el tamaño del rango destino.

Diferencias clave entre fórmulas matriciales clásicas y dinámicas

Las fórmulas matriciales clásicas requieren Ctrl + Mayús + Entrar, pueden resultar algo más difíciles de leer y, en muchos casos, están limitadas en cuanto a su capacidad de derramar resultados automáticamente, a diferencia de funciones modernas como BUSCARV y BUSCARX.

Las fórmulas de matrices dinámicas se escriben como fórmulas normales, se confirman solo con Intro y derraman los resultados por sí mismas, sin seleccionar rangos previos ni usar fórmulas de matriz heredadas.

Otra diferencia importante es que las funciones dinámicas devuelven matrices de forma explícita y se esperan como tal; si en un libro antiguo se utilizaba una función que devolvía una matriz a varias celdas, Excel podía aplicar una intersección implícita silenciosa.

Con las matrices dinámicas, Excel marca esos casos antiguos con el operador @, que indica dónde se estaba produciendo esa intersección implícita, para conservar el comportamiento previo y evitar resultados inesperados.

Conviene tener en cuenta también que las fórmulas de matrices dinámicas solo están disponibles en Excel 365 y Excel 2021; en versiones anteriores no funcionan y pueden aparecer como fórmulas matriciales heredadas si se abren esos libros en equipos sin soporte de matrices dinámicas.

Configurar y usar fórmulas de matrices dinámicas

Para utilizar una fórmula dinámica, basta con elegir la celda de inicio, escribir la fórmula con una función como FILTRAR u ORDENAR y pulsar Intro. Excel derramará automáticamente los resultados hacia abajo y hacia la derecha.

Es importante asegurarse de que haya espacio libre alrededor de la celda de inicio, porque si las celdas donde debería volcar la matriz ya contienen datos, Excel mostrará un error de desbordamiento (#DESBORDAMIENTO o similar).

Una vez creada la fórmula, el rango desbordado actúa como un bloque: si modificas la fórmula en la celda principal, se actualizan todos los resultados; si quieres borrar todo, basta con eliminar la fórmula de esa celda.

También puedes referirte al rango desbordado desde otras fórmulas usando el operador de desbordamiento (por ejemplo, =SUMA(F2#)), de forma que, si crece o reduce su tamaño, las fórmulas que lo utilicen se adaptarán automáticamente.

En entornos de programación, bibliotecas como Aspose.Cells permiten establecer y recalcular fórmulas de matrices dinámicas por código, usando métodos específicos para asignarlas a una celda y refrescarlas antes de realizar el cálculo general de fórmulas.

Aplicaciones avanzadas de matrices: álgebra lineal y finanzas

El trabajo con matrices en Excel no se limita a sumar rangos o a filtrar valores: también se puede usar para problemas de álgebra lineal y optimización, como inversión de matrices, resolución de sistemas de ecuaciones o construcción de carteras de inversión.

Una matriz cuadrada A se puede invertir en Excel mediante la función MINVERSA, que requiere una fórmula matricial (o dinámica, según la versión) sobre un rango de igual tamaño que la matriz original.

Para obtener la inversa de una matriz 3×3 situada en B3:D5, seleccionarías un bloque 3×3 vacío, escribirías =MINVERSA(B3:D5) y confirmarías como fórmula matricial, logrando así la matriz A^-1.

Si multiplicas la matriz original por su inversa usando MMULT sobre un rango apropiado, obtendrás una matriz identidad, análoga a multiplicar un número por su inverso, que siempre da 1.

Del mismo modo, puedes plantear un sistema de ecuaciones lineales en forma matricial, con A como matriz de coeficientes, K como vector de incógnitas y P como vector de términos independientes, y resolverlo con la relación K = A^-1 · P empleando MINVERSA y MMULT.

En finanzas, este enfoque matricial se aplica, por ejemplo, a problemas de optimización de carteras, donde se usa la matriz de covarianzas σ_ij entre títulos, los rendimientos esperados μ_j y restricciones de rentabilidad para encontrar la combinación de activos con menor riesgo para un objetivo de rentabilidad concreto.

A partir de la función de Lagrange y la derivación de las condiciones de primer orden, se llega de nuevo a un sistema matricial del tipo A·X = P, cuya solución X = A^-1·P nos da los pesos óptimos de cada activo en la cartera.

En un ejemplo con tres acciones A, B y C, con covarianzas y rendimientos esperados dados, se puede determinar un vector de inversiones tal que la cartera obtenga un 4% de rendimiento esperado con la varianza mínima, resultando en una combinación que aprovecha la diversificación para reducir el riesgo frente a invertir en un solo título.

Todo esto se implementa con las mismas herramientas básicas: MINVERSA, MMULT y fórmulas matriciales, reforzando la idea de que Excel puede ser una plataforma muy competente para análisis numérico cuando se domina el uso de matrices.

Tras recorrer desde los fundamentos de las fórmulas matriciales clásicas, pasando por las constantes de matriz y las matrices dinámicas, hasta los usos avanzados en álgebra lineal y finanzas, queda bastante claro que aprender a manejar bien las matrices en Excel es una inversión que te permite trabajar más limpio, más rápido y con soluciones que muchas veces están fuera del alcance de las fórmulas convencionales.